Template & Tips
1. 找模糊值 first or last occurrence, 二分法
int left = 0;
int right = nums.length - 1;
// find first occurrence
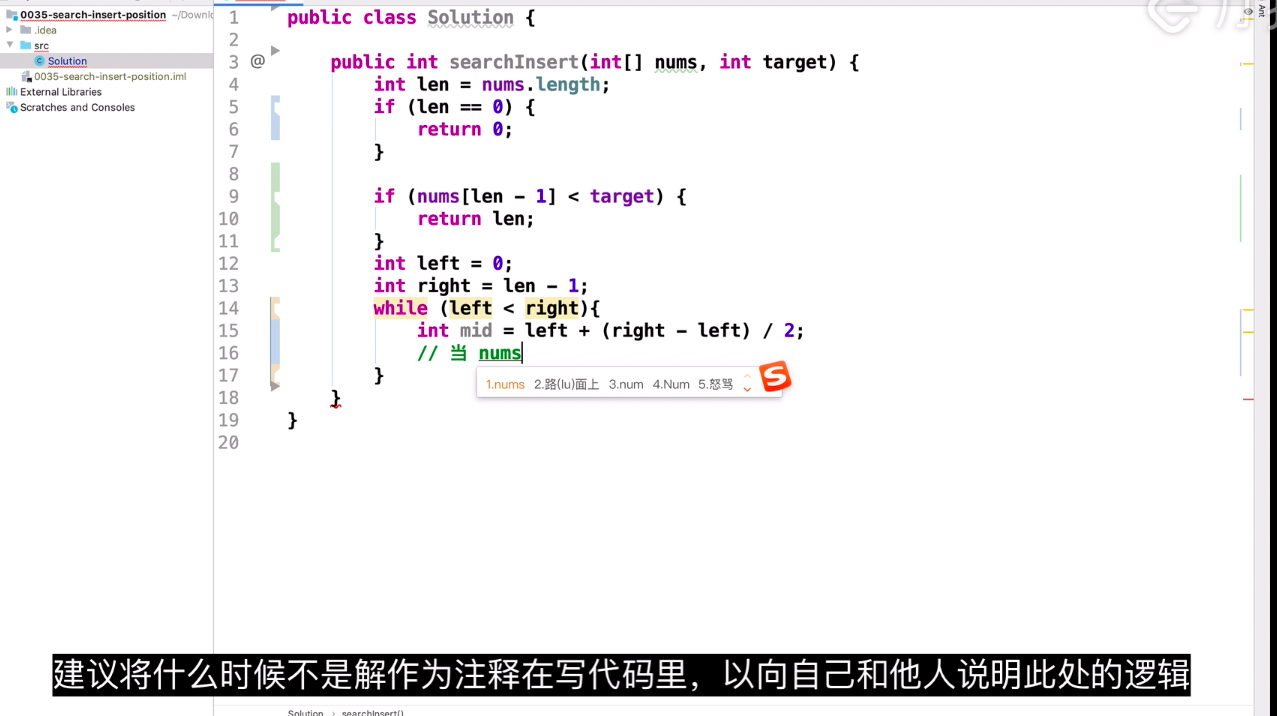
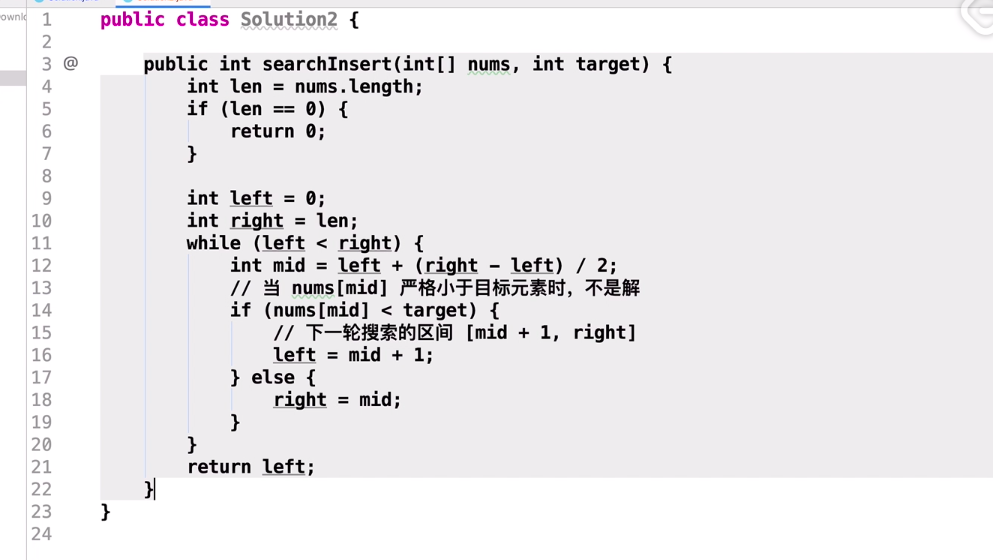
while (left < right) {
int mid = left + (right - left)/2;
if (nums[mid] < target) { // 往右半部找
left = mid + 1;
} else { // 往左半部找
right = mid;
}
}
return left; // right
// find last occurrence
while (left < right) {
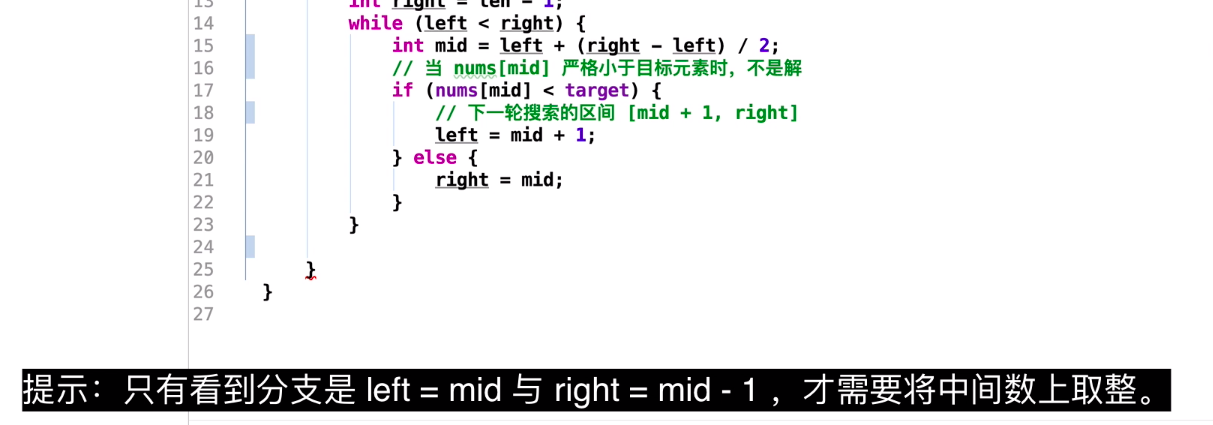
int mid = left + (right - left + 1)/2; // notice! +1
if (nums[mid] > target) { // 往左半部找
right = mid - 1;
} else { // 往右半部找
left = mid;
}
}
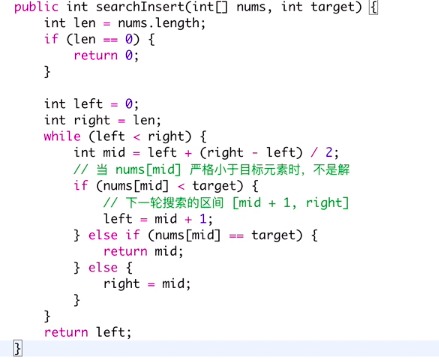
return left;2. 找確切值, 三分法, template,
3. 找最近似值 (closet to ...)
find peak (162)
Rotated
Mini in Rotated
二分法
二分查找 tips
decrease and conquer template
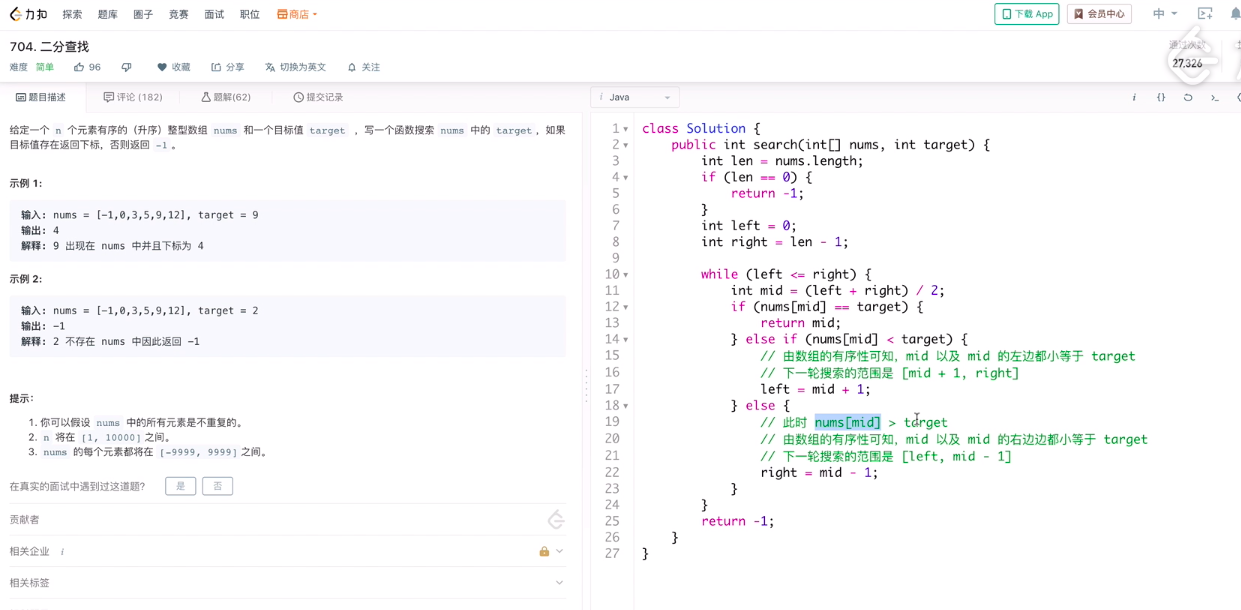
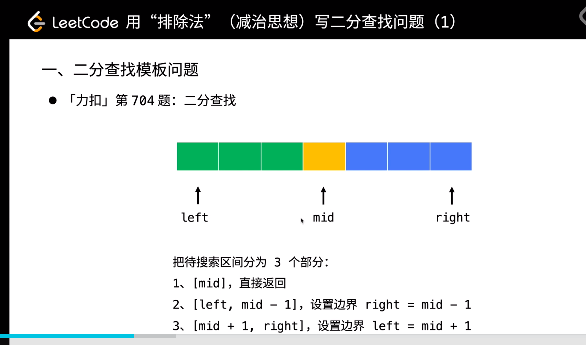
另一種做法
decrease and conquer, 朝排除 mid 思考, 分為兩部份


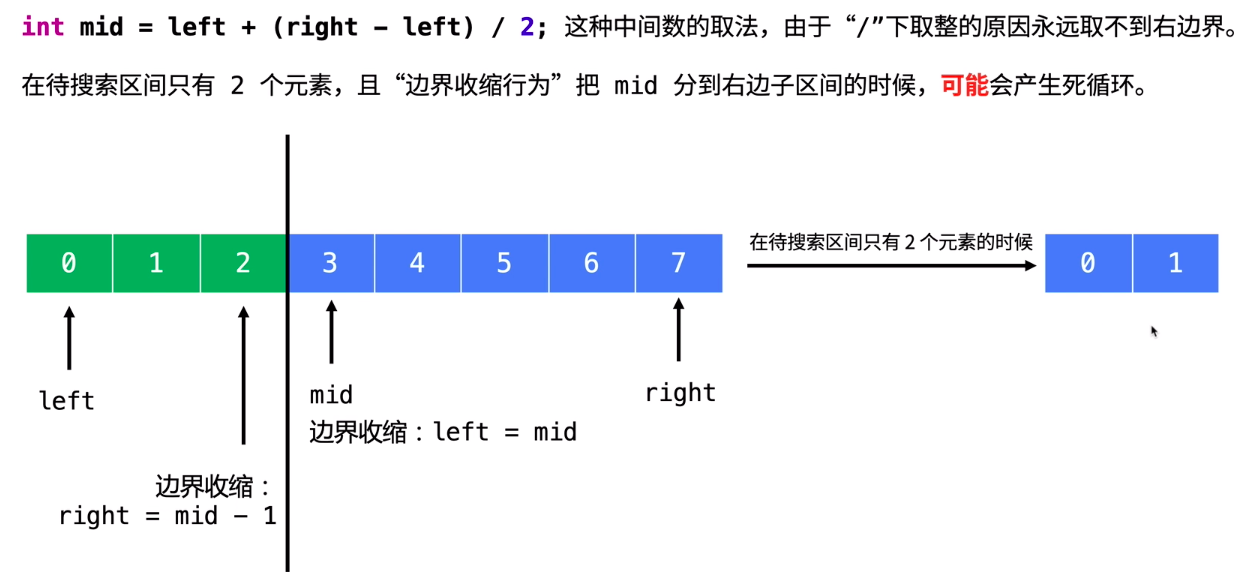
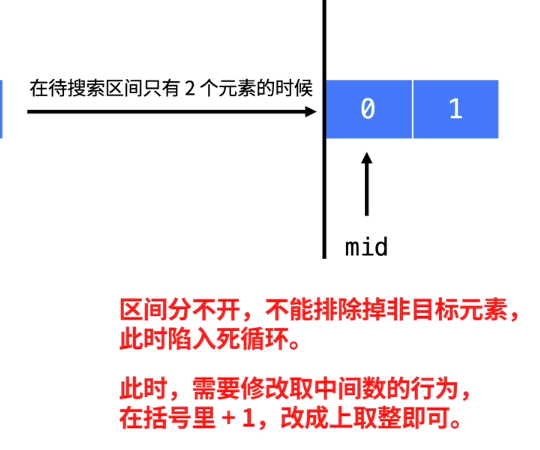


Last updated
